現在の情報化社会を支える大事な要素といえばコンピュータですが、そのコンピュータは人間とは数の数え方が違います。
コンピュータについてそれなりに知識のある人なら、0と1の2種類しか使わない2進数を扱っていることはご存じでしょう。
しかしコンピュータの世界では2進数の他に、16進数という数え方もよく出てきます。
2進数だけでも意味不明なのに16進数も出てきて、結構複雑です。
16進数と10進数、互いにどういった方法で変換されるのかが気になりますね。
またそもそもなぜ16進数まで使う必要があるのか?それぞれ詳しく見ていきましょう!
16進数とは?

16進数(または十六進法ともいう)とは、0、1、2、3、4、5、6、7、8、9の10個の数字と、A、B、C、D、E、Fの6つのアルファベットを用いた記数法のことです。
難しい言い方をすると、16を底とする位取り記数法となりますが、単純に各桁が16になると桁上がりする数字と考えてもOKです。
しかし16ごとに桁上がりするということは、10進数にあたる10~15までの6つの数字も1桁で表わさないといけません。
そこで出てくるのが先ほど紹介した、A~Fの6つのアルファベットです。
この6つのアルファベットを、以下のように10~15の数字に対応させることで、0~15までの数字を全て1桁で表現できます。
- 0→0
- 1→1
- 9→9
- 10→A
- 11→B
- 12→C
- 13→D
- 14→E
- 15→F
- 16→10
・
・
・
15(F)まで進んだら、桁が1つ上がるので、“10”となります。すなわち16進数で表記された“10”は、10進数でいうところの“16”です。
3桁目の“100”になるには、“FF”を1つ上げた時です。
“FF”は10進数でいうと、“255”に相当します。
255は「16²-1」なので、16²=256→100となります。
16,256,・・・と「16のn乗」ごとに、桁が1つずつ増えていることがわかりますね。
これは10進数と同じ考えです。10進数では10,100,1000,10000・・・と「10のn乗」の時に桁が1つずつ増えます。
1桁左に書かれた数字は、その右の数字よりも16倍の重みがあるということです。
ここまでが16進数の基礎となります。
次からは、16進数で表記された数字を10進数に、10進数で表記された数字を16進数に変換するための方法を具体的に解説していきます。
16進数から10進数への変換
まずは比較的簡単な16進数から10進数への変換からです。
実はこの変換のやり方については、以前投稿した2進数と10進数についての記事で紹介しているやり方とほぼ同じです。
2進数と10進数の変換!2の累乗数も覚えておけば楽になる?
では具体例を使って解説していきます。
「1005CF」と表記された16進数の数字があります。(因みに16進数の数字は、先頭に0xを目印として付けます。)
この数字を10進数に変えるには、2進数の変換と同様で、各桁の数字に重みを掛けて、全て足し合わせます。
2進数の重みは「2の(n-1)乗」でしたが、16進数では「16の(n-1)乗」となります。
以上を踏まえた上で「0x1005CF」については
- 6桁目の数字は1なので、1×16⁵=1048576
- 5桁目の数字は1なので、0×16⁴=0
- 4桁目の数字は0なので、0×16³=0
- 3桁目の数字は1なので、5×16²=1280
- 2桁目の数字は0なので、C×16¹=192(Cは12)
- 1桁目の数字は1なので、F×16⁰=15(Fは15)
となるので、全て足し合わせれば
1048576+0+0+1280+192+15=
1050063
となります。
これで16進数から10進数への変換は完了です。
2進数と違って、16の累乗やアルファベットも出てくるので少しややこしいですね。
10進数から16進数への変換
次は逆のパターンとなる10進数から16進数への変換です。
こちらは少しややこしくなります。
基本となるのは2進数の時に紹介したやり方と全く一緒で、要は10進数の数字を商が0になるまで16で割り続ければよい、ということになります。
今回もわかりやすいように、先ほどの例で用いた「1050063」で解説します。
この「1050063」が逆変換で、16進数の「0x1005CF」と一致することを確かめましょう!
詳しい説明は省いて、まずは以下のように商が0になるまで16で割り続けます。
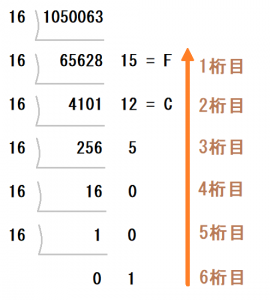
- 1050063を16で割って、商が65628、余りが15(=F)
- 65628を16で割って、商が4101、余りが12(=C)
- 4101を16で割って、商が256、余りが5
- 256を16で割って、商が16、余りが0
- 16を16で割って、商が1、余りが0
- 1を16で割って、商が0、余りが1
余りの数字を下から順番に並べると、「1005CF」となります。
※ただし余りが2桁の数字になっている部分は、さらに1桁に直す必要があります。上の例では、12と15をそれぞれCとFに変換させましょう。
16の累乗数を使って簡単に変換!
上で紹介したのはあくまで基本的な方法でした。
このやり方も実は16の累乗数をある程度覚えることで、比較的簡単に変換できます。
先ほどと同じ「1050063」で解説しますと、16進数から10進数に変換した時に以下のような形になりましたね。
1050063=1048576+0+0+1280+192+15
=1×16⁵+0×16⁴+0×16³+5×16²+12×16¹+15
やはり16の累乗数の和で表現出来てますね。
6番目の桁数は1、5と4番目の桁数は0、3番目の桁数は5、2番目の桁数はA、1番目の桁数はFで確定します。
以上から
1050063⇒⇒1 0 0 5 12 15⇒1005CF
と変換できることになります。
では今度は「5003」という数字を16進数に変換してみましょう!
16の累乗数を使って表現すると、
5003 =4096+907
=4096+3×256+139
=4096+3×256+8×16+11
=1×16³+3×16²+8×16¹+11×16⁰
各桁ごとに数字を割り振れば「5003」は
5003⇒0x138B
となりますね。
- 16¹= 16= 0x10(16進数)
- 16²= 256= 0x100(16進数)
- 16³= 4096= 0x1000(16進数)
- 16⁴= 65536= 0x10000(16進数)
- 16⁵= 1048576= 0x100000(16進数)
だいたい上の5つを暗記しておけば、10進数の数字を16進数に変換する際に役に立ちます。
特に16の4乗=65536は、2の32乗と同じでこれは頻出です。
6乗以上となるとかなり巨大な数字になるので、余力がある方だけ覚えてください(;^^)
小数点以下はどう表記する?

これまでは整数のみの変換を扱ってきました。しかし整数だけでなく、時には小数も扱わなければいけない場面は出てきますね。
10進数で小数点以下の数字を16進数に変換するにはどうすればよいでしょうか?
難しい話となるので敢えて簡単に解説しますが、やり方としては「小数部が0になるまで16倍し、答えの整数部分を上から並べる」と覚えましょう!
整数の10進数を16進数に変換した時は16で割りましたが、小数点以下の時は掛け算になるのです。
例えば、「0.84375」という数字を16進数に変換するには
- 0.84375×16=13.5(13=D)
- 0.5×16=8.0
つまり
0.78125⇒「0.D8」
では次は逆のパターンで見てみましょう。
「0.D8」と表記された16進数を10進数に変換するには、単純に小数点以下の「D8」の部分を10進数に変換するだけです。
ただしここで注意すべきは小数点以下の桁数です。
上の例では小数点以下が2桁だけですね。
この場合は最上位の桁の重みは「16の2乗」となり、2桁目の重みは「16の1乗」となります。
すなわち
D8⇒13×16²+8×16¹=216
となります。
ただしここで答えとなった小数点以下の216という数字は、0.84375と一致していないですね。
ではやり方が間違っているのかと言いますとそうではなくて、実はさらに216という数字を256で割ることが必要になります。
16進数「0.D8」の小数点以下の数字の意味とは、「256(16の2乗)分の量がD8(=216)ある」ということと同義です。
すなわち
216/256=108/128=54/64=27/32=0.84375
となるので、10進数と一致します。
ぶっちゃけここの部分は凄くややこしいですね。16進数のみならず、2進数でも小数点以下の変換はかなり戸惑うと思います。
相当数問題などをこなして慣れるしかないですね(;-_-)
16進数を使う場面とは?
16進数は2進数に比べるとややマイナーかもしれませんが、情報学においてはよく出てくる用語です。
代表的なのがhtmlのカラーコードですね。赤色なら#ff0000、青色なら#0000ffとして表現されます。
簡単に言いますと、htmlのカラーコードはRGB値と呼ばれ、最初の2桁が赤、真ん中の2桁が緑、最後の2桁が青の6桁になっています。
それぞれが16進数で設定されているので、「16⁶-1」通りの色が理論上表現できる形です。
他にもパソコンならIPアドレスの表記にも用いられますね。
さらにデータをオクテット形式(二進表記の8桁)で表現する際には、16進数で表すのが一般的で、利便性を高める意味でも16進数は重要となってきます。
まとめ
今回は16進数についての解説でした。やや難解な感じになったかもしれませんが、参考になりましたら幸いです。
16進数は2進数に比べるとアルファベットのA~Fまで出てくるので、慣れない内はややこしく感じます。
ただコンピュータの世界でAやFと一緒に数字が表記されていたら、十中八九16進数が関係している数字だとわかってきます。
特にゲームプログラミングでは数値のオーバーフロー関係でよくお世話になります。
ある程度プログラミングをかじった人なら、乱数や番地として255や65535なんていう数字が出てきますが、いずれも2のn乗や16のn乗、さらに8のn乗も関係してきます。
2進数と16進数はプログラミングをマスターしたい方にとっては必要不可欠でしょう。
変換も駆使すれば自分自身の計算能力も高まるので、頭の体操としても最適ですよ!