コンピュータは我々人間と違って、数値を2進数で取り扱っています。
2進数とは「0」か「1」で表記する記法ですが、単純に2種類の数字のみで表わされている点以外にも10進数と大きく違う点があります。
それがマイナスの表現です。
マイナス、すなわち負数とは中学の数学の時間で習うと思いますが、2進数でマイナスを表現しようとするとかなり変わったやり方をしないといけないんですよね。
一体どういったやり方なのでしょうか?気になる方はぜひご覧ください!
2進数でマイナスを表現するには?

まずは10進数でマイナスの数を表現する場合を考えます。
10進数でのマイナスの表記はすごく簡単で、数字の前に記号の“-”をつければOKです。
数字の「5」は、プラス(正)だと「+5」、マイナス(負)だと「-5」となります。
しかし2進数だと、プラスとマイナスの記号をつけるというやり方は駄目なのです!
10進数の「5」は2進数で「101」となるのですが、
- +101
- -101
としては駄目ということです。
※2進数と10進数の詳しい変換については以下の記事をどうぞ!
2進数と10進数の変換!2の累乗数も覚えておけば楽になる?
ではどう表現すればいいのか?ということについてですが、やり方は主に以下の2種類あります。
- 最上位の桁のビットを符号ビットとして表現する
- 2の補数を用いて表現する
この2種類あるのですが、順番に解説していきますね。
符号ビットを用いる方法
これは簡単に言いますと、先頭の桁でマイナスとプラスを分ける表現法となります。
例えば8ビットの2進数を考えてみましょう。
8ビットとは「2の8乗-1(0~255)」までの数字が2進数で表記できるのですが、先頭の桁を符号ビットとして用いるとした時に、「0」ならプラスの数、「1」ならマイナスの数となります。
- 0000 0000:0~+127
- 1000 0000:-128~-1
符号ビットとして用いない場合は、「0~255」までの数字だったのですが、先頭の桁でプラスかマイナスかを分けるので、それぞれ128個の数字が表現できます。
※“0”についてはマイナスもプラスも存在しませんが、便宜上“-128”として取り扱います。
- 00000000(⇒0)⇔10000000(⇒-128)
- 00000001(⇒1)⇔10000001(⇒-127)
- 01111111(⇒127)⇔11111111(⇒-1)
・
・
・
このような表現方法を『絶対値表現』と呼ぶのですが、実は現代のコンピュータではほぼ使用されていません。
絶対値表現の代わりに、次の章で紹介する『2の補数』を用いてマイナスを表現しています。
2進数でプラスとマイナスの記号を単純につけては駄目だと説明しましたが、この理由について簡単に解説します。
10進数の5のマイナスが「-5」になるのは、
+5 -5 = 0
のように計算してちょうどゼロになるからです。
すなわちマイナスの数と言うのは、引き算したらちょうどゼロになる数、ということなのですが、コンピュータ内部では引き算ではなく全て足し算とするからです。
実際上で紹介した8ビットの絶対値表現で考えてみましょう。
「+2」と「-128」という2つの数字があった時に、我々人間は
+2 -128 = -126
と普通に計算していますが、コンピュータ内部では引き算ができないので、普通に足し算します。
実際に2進数に変換して足してみると
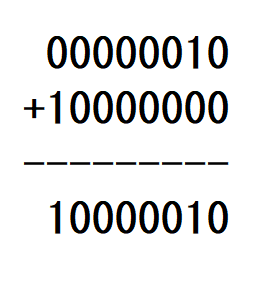
となるのですが、「10000010」は10進数で「-126」で確かに一致していることがわかります!
補数を使ってマイナスを表現!
それでは『補数』でマイナスを表現する手法を解説していきます。
しかしいきなり2進数で解説しても混乱するので、まず10進数で補数について簡単に解説します。
10進数の補数とは?
例えば10進数で「+37」という数字があった時に、マイナスの数字は
+37 -37 = 0
なので、単純に「-37」と算出できます。
しかし先ほども紹介したように、コンピュータでは引き算はできませんので、足し算として考えないといけません。
「+37」という数字を足し算で「0」にするには、どうすればよいのでしょうか?
ここで登場するのが補数の考え方です。
「+37」は2桁の数字ですが、この場合足し算をして、最上位の桁を無視した時にゼロになるような数字を考えるというやり方となります。
2桁の数字の場合は3桁目を無視して0になればいいので、足して100になる数字が補数ということになります。
「+37」に足すと100になるのは「63」です。
よって「63」が「-37」を表す補数になります。
2進数の補数とは?

さてこの補数の考えを2進数に置き換えるわけですが、実は2進数には「1の補数」と「2の補数」の2種類があります。
詳しい解説はここでは省かせて頂きますが、代表的なのは後者の「2の補数」を用いるやり方です。
では10進数と同じで、例として「-37」の2の補数を考えてみます。
まず「37」を2進数に変換すると「100101」となります。
次に変換した2進数の「1」と「0」をそれぞれ反転させます。
最後に「1」をプラスさせた数字が、求めたい2の補数となります。
- 37 ⇒ 100101
- 100101 ⇒ 011010
- 011010 + 1 ⇒ 011011
最終的に求められた「011011」ですが、実際に計算して見ると以下のように各桁で桁上がりの「1」が加えられて、全て「0」になり、7桁目で「1」になっています。

最上位の桁を無視すれば、全ての桁が「0」になっているので、これで改めて「-37」の2の補数となることがわかります。
因みに余談ですが、「011011」という数字を10進数に直すと、「27」となります。
10進数で「37」の補数は「63」でしたが、2進数では全然違うことがわかりますね。
これも理由は単純で、要は2進数の場合は、足し合わせた時にちょうど「2のn乗」の数字になっているのです。
上の例では、ちょうど6桁の2進数だったので、2の6乗=「64」の数字になれば、2の補数ということになります。
実際に「37」に「27」を足すと、
37 + 27 = 64
となりますね。
桁数は何桁でもいい?
ここで気づくと思いますが、最初に指定する桁数によって補数の値が変わってきます。
先ほどは6桁の2進数で考えましたが、例えば最初の「100101」を7桁で表現して、「0100101」とすると、「1011010」が反転した数字で、これに1を足すと
1011011 ⇒ 91
となって「91」が「-37」の2の補数となっています。
よって「37」と「91」を足すと「128=2の7乗」となることがわかります。
同様に、8桁(8ビット)で表現されると「219」、9桁で表現されると「475」がそれぞれ補数となっています。
1桁増えるごとに2のn乗分加算されていることがわかりますね。
“2の補数”と言われたら、「2のn乗から引いて、後はその数字を2進数に変換!」と覚えておけば凄く簡単でしょう。
まとめ
今回は2進数のマイナス表現についての解説でした。参考になりましたら幸いです!
大事なのはコンピュータ内部では我々人間と同じように、プラス・マイナスに分けて考えておらず、補数を用いているということです。
コンピュータの数値計算は改めて奥が深いとわかりますね。