地球に住んでいる我々にとっては、切っても切り離せないのが重力という存在ですね。
地球で生活している生き物はこの重力から逃れることはできず、どれだけ高くジャンプしても絶対に地面に落下します。
ところで似たような言葉で引力というのもありますね。
日常生活においては、ジェットコースターに乗った時にかかるG、月との間に働く引力で潮の満ち引きが起きることで、2つの言葉を使います。
学校の物理の授業でも習うと思いますが、おそらくニュートンの万有引力が有名でそこから知ったという人も多いでしょう。
重力と引力、どっちも引っ張られる力という点では共通していて混同されがちですが、一体何が決定的に違うのでしょうか?
今回はこの2つの力の違いと関係性を詳しく教えます。学校の授業などにも是非役立ててください!
重力と引力の違いとは?
一言で「重力と引力って何がどう違うの?」と聞かれて、どう答えるべきか迷いますよね。
まずは簡単にですが、この2つの言葉の意味の違いを簡単に教えます。
- 重力とは、遠心力と引力を合わせた力
- 引力とは、2つの物体が互いに引き合う力
わかりやすく端的にまとめるとこうなります。
ポイントとなるのは、重力と言うのは地球上にある物体全てに働く力で、引力は場所を問わず互いに引っ張りあう力のことです。
ただし重力の意味については遠心力という言葉も出てきて、少しややこしいですね。
単純に場所が違うだけで、両方とも引っ張りあう力だと思っていたら、実は違っていたのです。
ということで、2つの力についてもっと詳しく見ていきましょう!
2つの言葉をそれぞれ英語で表現すると、
- 重力:gravity
- 引力:attraction or attractive force
となります。
重力について解説

まずは重力について解説します。Wikipediaを参照すると、重力の定義がもっと詳しく書かれていました。
- 地球上で物体が地面に落下する現象を引き起こすとされる力
- 物体の重さを作りだす要因
このように書かれているのですが、結局何が原因で地球上で重力が発生するのか、そこが大事ですよね。
一般的な物理学では、地球上の物体に働く重力は、地球の引力と自転によって生じる遠心力との合力を意味します。
すなわち重力をG、引力をF、遠心力をRとすると、重力Gは
G = F + R
の式で表現できます。
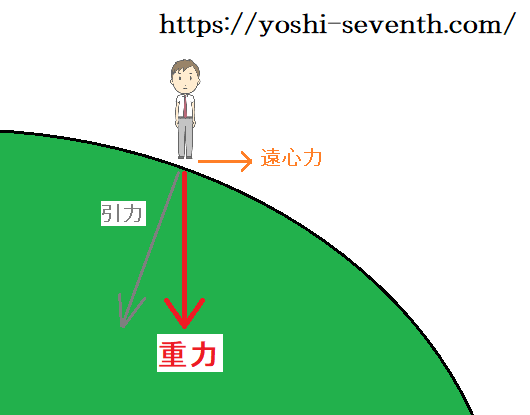
図で表現すると上のようになります。
ここで注意すべき点は、力には大きさと向きの2つの要素があることです。
上の画像を見た時に、重力Gは引力Fと遠心力Rの2つの辺で作られる、平行四辺形の対角線の一つをなしていますよね。
これは高校数学で習うベクトルの知識が絡んできます。
簡単に言えば、2つの力をベクトルAとBとみなした時、2つの力の合力はベクトルAとBの足し算になります。
このベクトルの足し算は、普通の数の足し算と違って、ただ数字を足し合わせるだけではなく、以下のような図で解釈する必要があります。
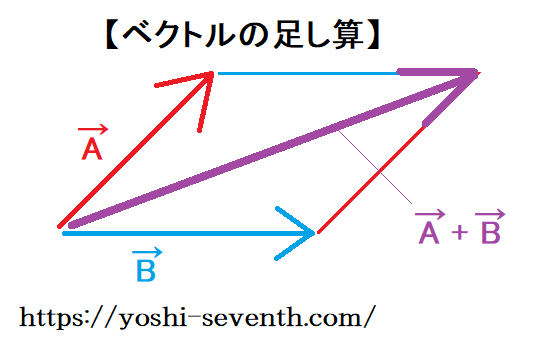
ベクトルAとベクトルBの2つの辺によって形成される平行四辺形の対角線、これがベクトルの足し算です。
ここでベクトルAが引力F、ベクトルBが遠心力Rに相当します。当然重力も力なので、この2つのベクトルの合成となるわけです。
ベクトルに関しては高校数学で詳しく学びます。高校数学を理解すればきっと物理もマスター出来ますよ!
遠心力って?
さて重力についての説明は以上でだいたい終わりなのですが、気になるのは遠心力の存在ですよね。
遠心力と言うのは回転している物体に働く力のことで、これは外に引っ張られる力を意味します。
地球自体も自転軸を中心に回転しているため、地球上にある全ての物体に遠心力が働きます。
水が落ちてこないのは、回転しているバケツに遠心力が働いて、中に入った水が外に引っ張られているのが原因で起きています。
しかし地球の遠心力は、実は地点によって大きさがバラバラなのです。(厳密に説明すると、地球内部の岩石の分布の違いで場所により差が出ます。)
地球は自転軸を中心に回転しているのですが、遠心力は自転軸に対して垂直に働き、赤道上で最も大きく、極地で最小(ほぼゼロ)となります。
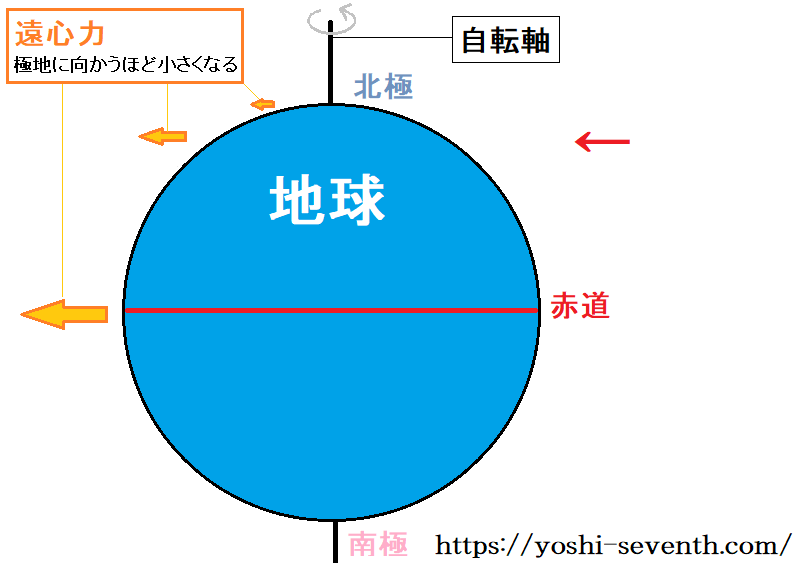
先ほどの重力の式をおさらいしますと、重力Gは引力Fと遠心力Rの足し算でしたね。
ここで注目してほしいのは、引力と遠心力の向きの違いです。
よく見ると、引力は地球が引っ張る力なので、地球の中心に向かっていますが、遠心力は外に引っ張られるので、引力とは向きが逆です。
これがベクトルの足し算の落とし穴で、向きが逆となっていることでマイナス、すなわち引き算と同じになってしまいます。
G=F-R
となるので、赤道上では重力は引力から遠心力を差し引いた値となります。つまり遠心力の分だけ重力は引力より小さくなるということです。
また上の画像を見てもらえればわかりますが、遠心力は赤道上で最も大きいので、これで赤道上の重力が地球の中で最も小さくなることも理解できます。
逆に北極や南極だと、遠心力がほぼゼロになるので、
G=F-R≒F
となり、ほぼ引力と等しくなります。
つまり赤道上の重力が最小で、極地の重力が最大となるわけです。
重力が最小になるということは体重も軽くなることを意味します、体重を少しでも誤魔化したい人は赤道上で体重計に乗りましょう(笑)
因みに遠心力は高い山の方が大きくなります、赤道上にある高い山に登ればもうダイエット不要でいいかも(;^^
引力について解説
さてこれまでは重力について解説してきました。
重力の解説の中で、「重力は引力と遠心力の足し算だ」と書きましたが、「そもそも引力とは一体何だ?」という話になりますよね(;^^
最初の章でも触れましたが、引力と言うのは「2つの物体が互いに引き合ってくっつこうとする力」を意味します。
一番わかりやすい例が、磁石ですね。
磁石のN極とS極を近づけると瞬時にくっつきます、まさに引力です。(磁石同士なので正確には磁力と呼びます。)

では肝心の地球の引力は、何が原因で生まれているのでしょうか?
地球に引力があるということは、何かと引っ張りあっていることになりますよね。
それは地球に最も近い位置を回っている星、すなわち月です。
地球と月との間では、互いに引っぱりあって巨大な引力が発生しています。
実は引力自体は全ての物体に働いているのですが、地球の引力の方があまりにも巨大すぎるので、ほとんど日常では感じません。
万有引力とも言うのですが、これを発見したのがかの有名な物理学者ニュートンです。

彼の考えでは、次の2つの法則が判明しました。
- 地球上にある全ての物体は、地球と引っ張り合っていること
- 質量のある物体なら、宇宙のどこでも相互に引っ張り合っている力が発生していること
もし万有引力の法則がなかったら、天体運動もまともに観測できなかったので、ニュートンは本当に偉大な発見をしたわけです。
月の引力で何が起きる?
引力はその物体の質量に比例して大きくなります。
地球と綱引きをしている月も巨大な天体なため、地球との間で巨大な引力を生じさせます。
これの最たる例が海の満潮や干潮です。
潮の満ち引きが起きるのは月の引力が大きく関係しています。
干潮の時には、海が月に引っ張られることで潮が引き、満潮の時には逆に月に引っ張られないことで潮が戻るわけです。
ニュートンは確かにリンゴが木から落ちるのを見たわけですが、それを見て「リンゴに重力が働いている」と悟ったわけではありません。
正しくは「リンゴに働いている力が、月や惑星でも働いているんじゃないか?」と想定したわけです。
まとめ
以上、重力と引力の違いと関係について述べてきました。それでは今回の内容をおさらいしましょう!
- 重力は引力と遠心力の合力
- 重力は赤道上で最小、極地で最大となる
- 引力は2つの物体が互いに引っぱり合いくっつこうとする力
- 月の引力で潮の満ち引きが起きる
- 「万有引力の法則」は重力を発見したわけではない
長い間やや混同していた、重力と引力の違い、これでかなりスッキリ理解できましたでしょうか?
物理の授業でもこの2つの違いを理解することは大事になります、ぜひマスターしましょう!