大学入試を控える受験生にとって大事な指標となるのが偏差値です。
偏差値とは簡単に言えば自分が全体の中でどのくらいの順位にいるのかを示した値で、平均値とはまた違います。
自分も高校生の時に偏差値の意味についてはあまりよくわかりませんでした。なんとなく数値が高ければ高いほどいいんだろうという認識を持っていただけです、そんなこと気にするよりも毎日の勉強の方が必死でしたからね。

ただし何も知らないよりは知っていたほうがある程度は便利です。
偏差値は大学入試を控える受験生にとっては知っておくに越したことはないのでこれを機会に知っておきましょう。
ついでに自分の偏差値の簡単な求め方も細かく解説していきます、ぜひ参考にしてみてください!
偏差値の意味について
まずは偏差値の意味についておさらいしておきます。
偏差値というのは、ある数値がサンプルの中でどのくらいの位置にいるかを示した無次元数のことです。数学的に言いますと平均値が50、標準偏差が10となるように標本変数を規格化したものです。
大学で確率統計の講義を習った人ならわかると思いますが、大半の人はこれだけの説明ではわからないと思います。もっと簡単に説明しますと、平均を50とした点数でテストの成績を見るという方法だと思ってください。

例えば100点満点の数学のテストを受けたときに、ある生徒Aの点数が60点だったとします。
この時に成績の良さがわかる方法としては、点数・順位・平均点を確かめる方法があります。仮に平均点が50点でAさんの順位が10位だったとします。
Aさんの点数=60 > 平均点=50 となってますので、この時点でAさんは平均より上、つまり良い成績だと分かります。
ぶっちゃけこれだけで十分だと思いますよね?なぜわざわざ偏差値という指標を使うのでしょうか?
理由は平均点と順位だけでは、その教科だけしか比べられないからです。上の例では数学のテストで説明しましたが、英語のテストだと話が変わります。
Aさんの英語のテストの点数が60点、順位が2位、平均点が30点だったとします。点数だけ見ると数学も英語も60点で成績は同じじゃん!と一言では言えません。
なぜなら平均点が異なるからです。
同じ100点満点でも数学の平均点が50点、英語の平均点が30点で英語の方が20点も低くなっています。数学は比較的易しかったので50点でしたが、英語は難しめだったので30点ということです。
順位に注目しますと、数学は10位、英語は2位となっているので、Aさんは英語のテストに関しては比較的成績が高めだということがわかります。
順位に関しても、選択科目が違っていたりするとテストを受ける生徒の数も変わってくるので単純には比較できません。
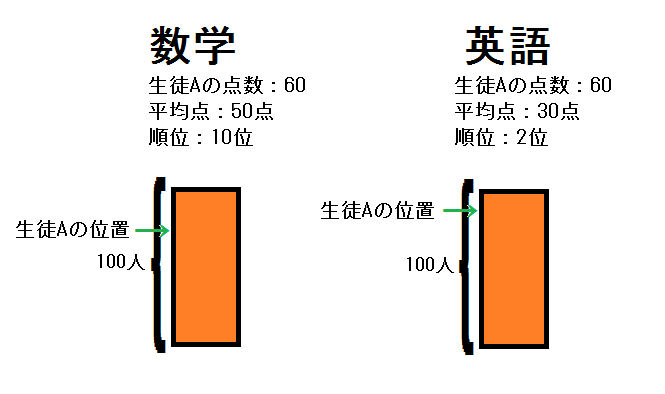
このように点数が同じでも平均点と順位で成績の良し悪しは変わってきます。
そこで代わりに登場したのが偏差値です。偏差値を使えば異なる科目の成績を統一して同じ物差しで比べられるので非常に便利です。
また受験生にとって一番知りたいのは全国データとの比較です。最終的に大学入試は全国生徒との競合になるので、当然必要となってきます。
仮に同じ試験を同じ高校内だけで受けるのと、他の高校も受けるのとでは全然意味が違ってきます。
当然平均点も違ってきますし、自分の高校で1位をとっても全国と比べると100位以内にも入らないかもしれません。
こういった全国規模で受ける試験は有名予備校が定期的に実施しています。
大学入試を控える受験生にとっては、河合塾や駿台予備校といった有名予備校の模擬試験は何度も受けたことがあるかもしれませんが、その度に自分の偏差値がわかります。
河合塾と駿台の比較!合格実績の違いが大きな鍵となる?
より具体的に言いますと、偏差値50がちょうど真ん中の位置にいて、それより低ければ平均より下、高ければ平均より上の位置にいるということです。
偏差値70以上が上位2%以内という狭き門ですが、ちょうど東京大学に合格しやすい偏差値がだいたい70前後なので目指す方は嫌でも70以上を目標しないといけません!
偏差値の簡単な求め方は?
偏差値は全体の中で自分がどの順位くらいなのかがわかる指標なので受験生にとってはぜひ知っておきたいものです。
その求め方について詳しく知りたい方も多いでしょうが、自分で求めなくても有名予備校の試験などでは成績表にちゃんと載ってあるので苦労はしません。
もちろん知っておくに越したことはありません、特に理系の方であれば偏差値というのは大学で習う確率論にも関係する内容しますし、そこまで難しい式じゃないので困惑する必要はありません。
では簡単な求め方の解説ですが、結論から言いますと偏差値は以下のような式で求められます。
偏差値=50 +{(得点-平均点)× 10} ÷ 標準偏差
ここで標準偏差という難しい言葉が出てきましたが、一体どういった値なのでしょうか?
実はこれに関して説明すると、それこそ大学の講義で習う確率論の話になります。厳密に言えば正規分布という内容ですが、かなり難しくなるので省略させていただきます。
前の項目で偏差値は統計学の知識があれば理解しやすいと説明しましたが、実は偏差値を求める際には標準偏差という値が必要になるのです。
標準偏差とはわかりやすく言えば、受験した生徒全体の点数のばらつき具合を示した数値です。
実はこの標準偏差は全ての生徒の点数がわからないと求められません。
仮に受験者数が100人、200人にもなれば一人一人の点数をExcelなどに入力してコンピュータで計算した値を求めないといけないので、手動で求めるというのはかなり時間がかかるし面倒です。
じゃあ求められないの?と思いがちですが、実は超簡単に求められる方法があります。それは標準偏差の値を20と置き換えることです。こうすれば上の公式は以下のように簡略化されます。
偏差値= 50 + (得点ー平均点) ÷ 2
何で20にして計算するの?と質問されてもちょっと説明が長くなるのでやはり省略させていただきます、要は複雑な数値計算を簡略化するための近似値だと思ってください。
ただしこの方法は、あくまで学校の偏差値を求める時限定のやり方です。
全国模試などは受ける生徒の数も莫大に増えてデータのバラつきが激しいため、標準偏差を20で計算するとかなりの誤差が生じたりしますので当てにしないように!
実際に計算してみよう!
では上に紹介した式を基にして実際に偏差値を求めてみます。
今回は1の項目で出てきた生徒Aの数学と英語の点数を例にして求めてみます。
- 数学:生徒A60点、平均点50点
- 英語:生徒A50点、平均点30点
先ほど紹介した簡略化した偏差値の式を基にして計算してみます。
英語の偏差値=50 +(50-30)÷2=60
つまり英語の偏差値の方が数学の偏差値よりも5点高いということなので、これで改めて英語の方が成績が上だと分かります。
このように偏差値は割と簡単に求められることがわかりました。ぜひみなさんもテストを受けたら自分の偏差値を求めてみてください!